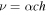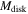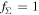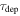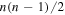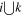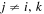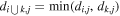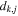Abstract
Celestial bodies with a mass of 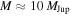 have been found orbiting nearby stars. It is unknown whether these objects formed like gas-giant planets through core accretion or like stars through gravitational instability. I show that objects with
have been found orbiting nearby stars. It is unknown whether these objects formed like gas-giant planets through core accretion or like stars through gravitational instability. I show that objects with  orbit metal-rich solar-type dwarf stars, a property associated with core accretion. Objects with
orbit metal-rich solar-type dwarf stars, a property associated with core accretion. Objects with 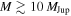 do not share this property. This transition is coincident with a minimum in the occurrence rate of such objects, suggesting that the maximum mass of a celestial body formed through core accretion like a planet is less than
do not share this property. This transition is coincident with a minimum in the occurrence rate of such objects, suggesting that the maximum mass of a celestial body formed through core accretion like a planet is less than 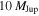 . Consequently, objects with
. Consequently, objects with 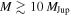 orbiting solar-type dwarf stars likely formed through gravitational instability and should not be thought of as planets. Theoretical models of giant planet formation in scaled minimum-mass solar nebula Shakura–Sunyaev disks with standard parameters tuned to produce giant planets predict a maximum mass nearly an order of magnitude larger. To prevent newly formed giant planets from growing larger than
orbiting solar-type dwarf stars likely formed through gravitational instability and should not be thought of as planets. Theoretical models of giant planet formation in scaled minimum-mass solar nebula Shakura–Sunyaev disks with standard parameters tuned to produce giant planets predict a maximum mass nearly an order of magnitude larger. To prevent newly formed giant planets from growing larger than 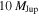 , protoplanetary disks must therefore be significantly less viscous or of lower mass than typically assumed during the runaway gas accretion stage of giant planet formation. Either effect would act to slow the Type I/II migration of planetary embryos/giant planets and promote their survival. These inferences are insensitive to the host star mass, planet formation location, or characteristic disk dissipation time.
, protoplanetary disks must therefore be significantly less viscous or of lower mass than typically assumed during the runaway gas accretion stage of giant planet formation. Either effect would act to slow the Type I/II migration of planetary embryos/giant planets and promote their survival. These inferences are insensitive to the host star mass, planet formation location, or characteristic disk dissipation time.
Export citation and abstract BibTeX RIS
1. Introduction
Celestial bodies with a mass of 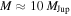 have been found orbiting nearby stars as well as floating freely in star-forming regions and the field (e.g., Latham et al. 1989; Zapatero Osorio et al. 2000; Kirkpatrick et al. 2006). Since it is currently impossible to determine the origin of a given
have been found orbiting nearby stars as well as floating freely in star-forming regions and the field (e.g., Latham et al. 1989; Zapatero Osorio et al. 2000; Kirkpatrick et al. 2006). Since it is currently impossible to determine the origin of a given 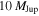 object, it is unknown whether these bodies formed like gas-giant planets through core accretion or like stars through gravitational instability. If it were practical to infer the typical mass separating objects formed through core accretion from those formed through gravitational instability, it would be possible to derive otherwise unobtainable constraints on planet formation models as well as the structure and properties of planet-forming disks (e.g., Tanigawa & Ikoma 2007; Tanigawa & Tanaka 2016).
object, it is unknown whether these bodies formed like gas-giant planets through core accretion or like stars through gravitational instability. If it were practical to infer the typical mass separating objects formed through core accretion from those formed through gravitational instability, it would be possible to derive otherwise unobtainable constraints on planet formation models as well as the structure and properties of planet-forming disks (e.g., Tanigawa & Ikoma 2007; Tanigawa & Tanaka 2016).
The existence of  objects both in orbit around stars and in isolation, combined with the ambiguity of their formation, has made it difficult to define a clear mass upper limit for planets. The IAU Working Group on Extrasolar Planets adopted the working definition of a planet as an object with a true mass below the limiting mass for thermonuclear fusion of deuterium that orbits a star or stellar remnant. On the other hand, substellar objects with true masses above the limiting mass for thermonuclear fusion of deuterium were defined as brown dwarfs, regardless of how they formed or where they are located (Boss et al. 2007). At solar composition, the minimum mass to significantly burn deuterium is thought to be near
objects both in orbit around stars and in isolation, combined with the ambiguity of their formation, has made it difficult to define a clear mass upper limit for planets. The IAU Working Group on Extrasolar Planets adopted the working definition of a planet as an object with a true mass below the limiting mass for thermonuclear fusion of deuterium that orbits a star or stellar remnant. On the other hand, substellar objects with true masses above the limiting mass for thermonuclear fusion of deuterium were defined as brown dwarfs, regardless of how they formed or where they are located (Boss et al. 2007). At solar composition, the minimum mass to significantly burn deuterium is thought to be near 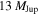 , independent of the formation channel (e.g., Grossman & Graboske 1973; Saumon et al. 1996; Burrows et al. 1997; Spiegel et al. 2011; Bodenheimer et al. 2013). Other definitions for giant planets referencing their intrinsic properties have also been proposed (e.g., Hatzes & Rauer 2015).
, independent of the formation channel (e.g., Grossman & Graboske 1973; Saumon et al. 1996; Burrows et al. 1997; Spiegel et al. 2011; Bodenheimer et al. 2013). Other definitions for giant planets referencing their intrinsic properties have also been proposed (e.g., Hatzes & Rauer 2015).
The definition of planets as objects with 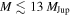 is problematic for several reasons. The critical mass for deuterium burning is not a step function, so it is also necessary to arbitrarily specify the fraction of the initial deuterium burned to uniquely define the critical mass. Since the critical mass depends on the composition, at
is problematic for several reasons. The critical mass for deuterium burning is not a step function, so it is also necessary to arbitrarily specify the fraction of the initial deuterium burned to uniquely define the critical mass. Since the critical mass depends on the composition, at 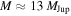 a metal-poor object would be a planet while a metal-rich object would be a brown dwarf. Because the mass required for deuterium fusion depends on the internal properties of an object, its calculation is necessarily dependent on imperfect models. Finally, the definition does not take into account the potentially unique ways such objects are formed.
a metal-poor object would be a planet while a metal-rich object would be a brown dwarf. Because the mass required for deuterium fusion depends on the internal properties of an object, its calculation is necessarily dependent on imperfect models. Finally, the definition does not take into account the potentially unique ways such objects are formed.
The elegance of a formation-based planet definition has been broadly recognized (e.g., Schneider et al. 2011; Wright et al. 2011; Chabrier et al. 2014). Under a formation-based definition, planets are celestial bodies that form through core accretion (Pollack et al. 1996; Hubickyj et al. 2005). Conversely, brown dwarfs and stars form through direct gravitational collapse, either at the disk or core scale (e.g., Adams et al. 1989; Bate et al. 2003; Bate 2012; Kratter & Lodato 2016). Despite the appeal of this definition, it has not been put into practice because of the difficulty in observationally determining the origin of individual celestial bodies orbiting distant stars.
Celestial bodies that form through core accretion and gravitational instability can be separated statistically though. Giant planets with a mass of 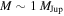 preferentially orbit dwarf stars that are metal-rich. This fact is thought to be indicative of formation through core accretion (Santos et al. 2004; Fischer & Valenti 2005; Sozzetti et al. 2006, 2009). This observational inference is supported by theoretical exoplanet population synthesis calculations, which suggest that the most massive objects formed through core accretion should be exclusively found around the most metal-rich stars (Mordasini et al. 2012). In contrast, gravitational instability is thought to occur with equal efficiency regardless of gas-phase metallicity (Boss 2002; Bate 2014). In accord with this idea, the occurrence of low-mass stars with
preferentially orbit dwarf stars that are metal-rich. This fact is thought to be indicative of formation through core accretion (Santos et al. 2004; Fischer & Valenti 2005; Sozzetti et al. 2006, 2009). This observational inference is supported by theoretical exoplanet population synthesis calculations, which suggest that the most massive objects formed through core accretion should be exclusively found around the most metal-rich stars (Mordasini et al. 2012). In contrast, gravitational instability is thought to occur with equal efficiency regardless of gas-phase metallicity (Boss 2002; Bate 2014). In accord with this idea, the occurrence of low-mass stars with 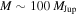 orbiting more massive stars like planets is independent of metal abundance (Latham et al. 2002; Carney et al. 2003). The maximum mass at which celestial bodies no longer preferentially orbit metal-rich solar-type dwarf stars can therefore be used to separate massive planets from brown dwarfs and establish the mass of the largest objects that can be formed through core accretion.
orbiting more massive stars like planets is independent of metal abundance (Latham et al. 2002; Carney et al. 2003). The maximum mass at which celestial bodies no longer preferentially orbit metal-rich solar-type dwarf stars can therefore be used to separate massive planets from brown dwarfs and establish the mass of the largest objects that can be formed through core accretion.
It has been impossible to confidently make this statistical separation in the past due to the lack of giant planets and brown dwarfs with mass estimates unaffected by the Doppler 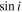 degeneracy orbiting solar-type dwarf stars with homogeneous stellar parameters. That comparison is now possible. In this paper, I calculate the mass at which transiting objects no longer preferentially orbit metal-rich solar-type dwarf stars. The transition occurs somewhere in the range of
degeneracy orbiting solar-type dwarf stars with homogeneous stellar parameters. That comparison is now possible. In this paper, I calculate the mass at which transiting objects no longer preferentially orbit metal-rich solar-type dwarf stars. The transition occurs somewhere in the range of 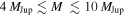 , suggesting that objects with
, suggesting that objects with  form through core accretion like giant planets, while objects with
form through core accretion like giant planets, while objects with  form like stars through gravitational instability. I describe my sample definition in Section 2. I detail my analysis procedures and compare my results to a model of the runaway gas accretion stage of giant planet formation in Section 3. I discuss the overall results and implications in Section 4 and conclude by summarizing my findings in Section 5.
form like stars through gravitational instability. I describe my sample definition in Section 2. I detail my analysis procedures and compare my results to a model of the runaway gas accretion stage of giant planet formation in Section 3. I discuss the overall results and implications in Section 4 and conclude by summarizing my findings in Section 5.
2. Sample Definition
I would like to calculate the mass at which secondary companions (e.g., planets, brown dwarfs, and low-mass stars) no longer preferentially orbit metal-rich solar-type dwarf primaries. I target systems where the minimum mass, 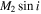 , of the secondary has been inferred with the Doppler technique and the inclination, i, of the orbit is known to be close to 90° because of the observed transit. That has two major advantages. First, the minimum mass inferred for the secondary in each system from the Doppler measurement is very close to the true secondary mass because the observed transit ensures that
, of the secondary has been inferred with the Doppler technique and the inclination, i, of the orbit is known to be close to 90° because of the observed transit. That has two major advantages. First, the minimum mass inferred for the secondary in each system from the Doppler measurement is very close to the true secondary mass because the observed transit ensures that 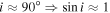 . Second, the observation of both the Doppler and transit signals virtually guarantees that the secondary is real and not a false positive.
. Second, the observation of both the Doppler and transit signals virtually guarantees that the secondary is real and not a false positive.
Using the application programming interface (API) call in Appendix A, I select from the NASA Exoplanet Archive all of the confirmed low-mass secondaries that have 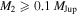 and have been detected with both the Doppler and transit techniques. I cross match that sample on R.A. and decl. with the catalog of homogeneously derived exoplanet host star stellar parameters from SWEET-Cat (Santos et al. 2013; Andreasen et al. 2017). Though I did not explicitly restrict the sample to solar-type dwarf primaries, the requirements imposed above produce a sample of primary stars with
and have been detected with both the Doppler and transit techniques. I cross match that sample on R.A. and decl. with the catalog of homogeneously derived exoplanet host star stellar parameters from SWEET-Cat (Santos et al. 2013; Andreasen et al. 2017). Though I did not explicitly restrict the sample to solar-type dwarf primaries, the requirements imposed above produce a sample of primary stars with 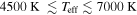 and
and 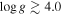 . I rescale all of the secondary masses from the NASA Exoplanet Archive sample using the uniformly calculated SWEET-Cat primary star mass scale. I include in Table 1 the secondary masses and primary metallicities of the resulting sample of 119 systems. Because of the transit requirement, 95% of the objects in Table 1 have an orbital period of
. I rescale all of the secondary masses from the NASA Exoplanet Archive sample using the uniformly calculated SWEET-Cat primary star mass scale. I include in Table 1 the secondary masses and primary metallicities of the resulting sample of 119 systems. Because of the transit requirement, 95% of the objects in Table 1 have an orbital period of 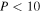 days and therefore a semimajor axis of
days and therefore a semimajor axis of 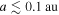 .
.
Table 1. Giant Planets and Brown Dwarfs that have Doppler-inferred Masses and Transit Solar-type Stars with Homogeneous Stellar Parameters from SWEET-Cat
| System | Simbad | R.A. | Decl. | Mass | Metallicity | Discovery | Stellar Parameter |
|---|---|---|---|---|---|---|---|
| Name | Reference | Reference | |||||
| (h m s) | (d m s) | ( ) ) |
|||||
| CoRoT-8 | CoRoT-8 | 19 26 21.243 | +01 25 35.17 |

|
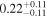
|
Bordé et al. (2010) | Mortier et al. (2013b) |
| HAT-P-12 | GSC 03033-00706 | 13 57 33.48 | +43 29 36.7 |
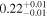
|
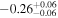
|
Hartman et al. (2009) | Andreasen et al. (2017) |
| WASP-29 | TYC 8015-1020-1 | 23 51 31.085 | −39 54 24.26 |
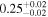
|
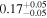
|
Hellier et al. (2010) | Mortier et al. (2013b) |
| WASP-21 | GSC 01715-00679 | 23 09 58.254 | +18 23 45.88 |

|
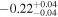
|
Bouchy et al. (2010) | Mortier et al. (2013b) |
| WASP-63 | TYC 7612-556-1 | 06 17 20.7489 | −38 19 23.773 |
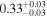
|
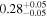
|
Hellier et al. (2012) | Mortier et al. (2013b) |
| HD 149026 | HD 149026 | 16 30 29.6185 | +38 20 50.308 |
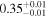
|
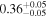
|
Sato et al. (2005) | Ammler-von Eiff et al. (2009) |
| WASP-94 A | WASP-94A | 20 55 07.946 | −34 08 08.00 |

|
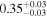
|
Neveu-VanMalle et al. (2014) | Andreasen et al. (2017) |
| WASP-67 | TYC 6307-1388-1 | 19 42 58.512 | −19 56 58.41 |
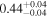
|
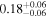
|
Hellier et al. (2012) | Mortier et al. (2013b) |
| WASP-11 | TYC 2340-1714-1 | 03 09 28.5432 | +30 40 24.853 |
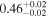
|
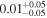
|
West et al. (2009b) | Mortier et al. (2013b) |
| WASP-17 | TYC 6787-1927-1 | 15 59 50.947 | −28 03 42.33 |

|
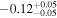
|
Anderson et al. (2010) | Mortier et al. (2013b) |
| WASP-31 | WASP-31 | 11 17 45.357 | −19 03 17.21 |

|
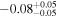
|
Anderson et al. (2011b) | Mortier et al. (2013b) |
| WASP-52 | WASP-52 | 23 13 58.76 | +08 45 40.6 |
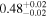
|
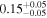
|
Hébrard et al. (2013) | Andreasen et al. (2017) |
| WASP-6 | TYC 6972-75-1 | 23 12 37.7380 | −22 40 26.261 |
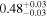
|
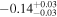
|
Gillon et al. (2009) | Mortier et al. (2013b) |
| HAT-P-46 | GSC 05100-00045 | 18 01 46.608 | −02 58 15.43 |
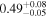
|
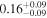
|
Hartman et al. (2014) | Andreasen et al. (2017) |
| TrES-4 | NAME TrES-4b | 17 53 13.058 | +37 12 42.36 |
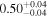
|

|
Mandushev et al. (2007) | Ammler-von Eiff et al. (2009) |
| CoRoT-5 | CoRoT-5 | 06 45 06.541 | +00 48 54.86 |
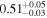
|
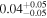
|
Rauer et al. (2009) | Mortier et al. (2013b) |
| WASP-13 | TYC 2496-1114-1 | 09 20 24.7098 | +33 52 56.717 |
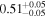
|
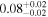
|
Skillen et al. (2009) | Chew et al. (2013) |
| WASP-42 | 2MASS J12515557-4204249 | 12 51 55.571 | −42 04 24.99 |
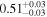
|
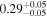
|
Lendl et al. (2012) | Mortier et al. (2013b) |
| HAT-P-1 | BD+37 4734B | 22 57 46.844 | +38 40 30.33 |
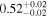
|
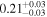
|
Bakos et al. (2007b) | Ammler-von Eiff et al. (2009) |
| HAT-P-17 | TYC 2717-417-1 | 21 38 08.7305 | +30 29 19.453 |
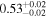
|
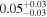
|
Howard et al. (2012) | Mortier et al. (2013b) |
| OGLE-TR-111 | V* V759 Car | 10 53 17.91 | −61 24 20.3 |
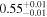
|
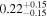
|
Pont et al. (2004) | Mortier et al. (2013b) |
| WASP-15 | TYC 7283-1162-1 | 13 55 42.705 | −32 09 34.66 |
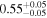
|

|
West et al. (2009a) | Mortier et al. (2013b) |
| WASP-62 | CPD-64 484 | 05 48 33.5918 | −63 59 18.372 |

|

|
Hellier et al. (2012) | Mortier et al. (2013b) |
| HAT-P-39 | GSC 01364-01424 | 07 35 01.979 | +17 49 48.30 |

|
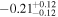
|
Hartman et al. (2012) | Andreasen et al. (2017) |
| WASP-25 | TYC 6706-861-1 | 13 01 26.374 | −27 31 19.94 |
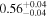
|
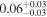
|
Enoch et al. (2011b) | Mortier et al. (2013b) |
| WASP-22 | TYC 6446-326-1 | 03 31 16.3274 | −23 49 10.852 |
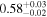
|
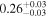
|
Maxted et al. (2010b) | Mortier et al. (2013b) |
| WASP-34 | CD-23 9677 | 11 01 35.8969 | −23 51 38.409 |

|

|
Smalley et al. (2011) | Mortier et al. (2013b) |
| WASP-55 | TYC 6125-113-1 | 13 35 01.9530 | −17 30 12.523 |
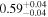
|
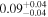
|
Hellier et al. (2012) | Mortier et al. (2013b) |
| HAT-P-27 | HAT-P-27 | 14 51 04.189 | +05 56 50.53 |
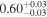
|

|
Béky et al. (2011) | Mortier et al. (2013b) |
| WASP-56 | Cl* Melotte 111 AV 561 | 12 13 27.8904 | +23 03 20.459 |

|
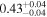
|
Faedi et al. (2013) | Mortier et al. (2013b) |
| XO-2 N | TYC 3413-5-1 | 07 48 06.468 | +50 13 32.96 |
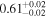
|
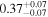
|
Burke et al. (2007) | Damasso et al. (2015) |
| OGLE-TR-10 | V* V5125 Sgr | 17 51 28.25 | −29 52 34.9 |
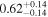
|
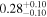
|
Konacki et al. (2005) | Santos et al. (2006) |
| WASP-54 | BD+00 3088 | 13 41 49.0281 | −00 07 41.036 |
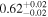
|
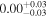
|
Faedi et al. (2013) | Mortier et al. (2013b) |
| K2-30 | UCAC4 562-007074 | 03 29 22.049 | +22 17 57.75 |
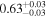
|
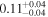
|
Johnson et al. (2016) | Lillo-Box et al. (2016) |
| HAT-P-24 | TYC 774-1441-1 | 07 15 18.0149 | +14 15 45.475 |
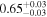
|

|
Kipping et al. (2010) | Andreasen et al. (2017) |
| HD 209458 | V* V376 Peg | 22 03 10.7728 | +18 53 03.550 |

|

|
Mazeh et al. (2000), Charbonneau et al. (2000), Henry et al. (2000) | Sousa et al. (2008) |
| HAT-P-30 | BD+06 1909 | 08 15 47.9792 | +05 50 12.359 |
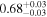
|
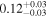
|
Johnson et al. (2011) | Mortier et al. (2013b) |
| WASP-35 | TYC 4762-714-1 | 05 04 19.6327 | −06 13 47.376 |
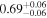
|

|
Enoch et al. (2011a) | Mortier et al. (2013b) |
| CoRoT-4 | CoRoT-4 | 06 48 46.715 | −00 40 21.98 |
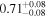
|
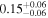
|
Aigrain et al. (2008) | Mortier et al. (2013b) |
| HAT-P-4 | BD+36 2593 | 15 19 57.9275 | +36 13 46.785 |
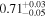
|
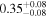
|
Kovács et al. (2007) | Ammler-von Eiff et al. (2009) |
| TrES-1 | NAME TrES-1b | 19 04 09.844 | +36 37 57.54 |
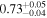
|

|
Alonso et al. (2004) | Santos et al. (2006) |
| HAT-P-41 | TYC 488-2442-1 | 19 49 17.4383 | +04 40 20.763 |
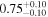
|
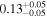
|
Hartman et al. (2012) | Tsantaki et al. (2014) |
| CoRoT-9 | CoRoT-9 | 18 43 08.810 | +06 12 14.89 |
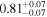
|
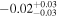
|
Deeg et al. (2010) | Mortier et al. (2013b) |
| CoRoT-12 | CoRoT-12 | 06 43 03.762 | −01 17 47.12 |
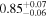
|
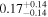
|
Gillon et al. (2010) | Mortier et al. (2013b) |
| WASP-16 | TYC 6147-229-1 | 14 18 43.922 | −20 16 31.85 |
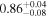
|
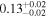
|
Lister et al. (2009) | Mortier et al. (2013b) |
| XO-1 | BD+28 2507 | 16 02 11.8470 | +28 10 10.421 |
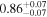
|

|
McCullough et al. (2006) | Ammler-von Eiff et al. (2009) |
| WASP-1 | TYC 2265-107-1 | 00 20 40.077 | +31 59 23.79 |
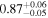
|
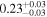
|
Collier Cameron et al. (2007) | Mortier et al. (2013b) |
| WASP-2 | WASP-2 | 20 30 54.130 | +06 25 46.37 |
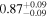
|
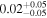
|
Collier Cameron et al. (2007) | Mortier et al. (2013b) |
| WASP-76 | BD+01 316 | 01 46 31.8590 | +02 42 02.065 |
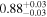
|
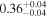
|
West et al. (2016) | Andreasen et al. (2017) |
| WASP-23 | GSC 07635-01376 | 06 44 30.65 | −42 45 41.0 |
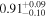
|
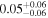
|
Triaud et al. (2011) | Mortier et al. (2013b) |
| WASP-28 | 2MASS J23342787-0134482 | 23 34 27.881 | −01 34 48.13 |
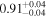
|

|
Anderson et al. (2015) | Mortier et al. (2013b) |
| WASP-41 | TYC 7247-587-1 | 12 42 28.497 | −30 38 23.55 |
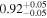
|
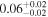
|
Maxted et al. (2011) | Mortier et al. (2013b) |
| WASP-79 | CD-30 1812 | 04 25 29.0162 | −30 36 01.603 |
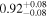
|
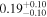
|
Smalley et al. (2012) | Mortier et al. (2013b) |
| WASP-78 | TYC 5889-271-1 | 04 15 01.5044 | −22 06 59.109 |

|
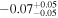
|
Smalley et al. (2012) | Mortier et al. (2013b) |
| WASP-7 | HD 197286 | 20 44 10.2190 | −39 13 30.894 |
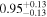
|
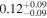
|
Hellier et al. (2009b) | Mortier et al. (2013b) |
| WASP-44 | GSC 05264-00740 | 00 15 36.770 | −11 56 17.30 |
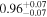
|
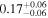
|
Anderson et al. (2012) | Andreasen et al. (2017) |
| WASP-58 | TYC 3525-76-1 | 18 18 48.2530 | +45 10 19.257 |
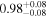
|

|
Hébrard et al. (2013) | Andreasen et al. (2017) |
| HAT-P-35 | TYC 203-1079-1 | 08 13 00.1827 | +04 47 13.382 |
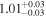
|

|
Bakos et al. (2012) | Mortier et al. (2013b) |
| OGLE-TR-182 | OGLE-TR 182 | 11 09 18.71 | −61 05 42.9 |

|

|
Pont et al. (2008) | Pont et al. (2008) |
| OGLE-TR-211 | 2MASS J10401438-6227201 | 10 40 14.39 | −62 27 20.2 |
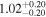
|
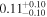
|
Udalski et al. (2008) | Udalski et al. (2008) |
| WASP-26 | TYC 5839-876-1 | 00 18 24.7001 | −15 16 02.287 |

|
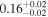
|
Smalley et al. (2010) | Mortier et al. (2013b) |
| WASP-24 | TYC 339-329-1 | 15 08 51.7355 | +02 20 35.953 |

|
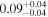
|
Street et al. (2010) | Mortier et al. (2013b) |
| HAT-P-6 | TYC 3239-992-1 | 23 39 05.8108 | +42 27 57.502 |
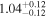
|

|
Noyes et al. (2008) | Ammler-von Eiff et al. (2009) |
| WASP-45 | TYC 6996-583-1 | 00 20 56.9941 | −35 59 53.756 |

|
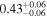
|
Anderson et al. (2012) | Mortier et al. (2013b) |
| HAT-P-42 | GSC 00232-01451 | 09 01 22.648 | +06 05 49.99 |
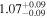
|

|
Boisse et al. (2013) | Andreasen et al. (2017) |
| WASP-82 | TYC 88-57-1 | 04 50 38.5600 | +01 53 38.088 |

|
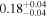
|
West et al. (2016) | Andreasen et al. (2017) |
| WASP-19 | GSC 08181-01711 | 09 53 40.077 | −45 39 33.06 |

|

|
Hebb et al. (2010) | Mortier et al. (2013b) |
| WASP-75 | GSC 05816-01135 | 22 49 32.568 | −10 40 31.93 |
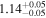
|
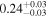
|
Chew et al. (2013) | Andreasen et al. (2017) |
| CoRoT-1 | CoRoT-1 | 06 48 19.172 | −03 06 07.68 |
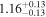
|
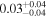
|
Barge et al. (2008) | Mortier et al. (2013b) |
| OGLE-TR-132 | V* V742 Car | 10 50 34.72 | −61 57 25.9 |
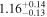
|

|
Bouchy et al. (2004) | Gillon et al. (2007) |
| WASP-95 | CD-48 14223 | 22 29 49.7348 | −48 00 11.012 |
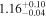
|

|
Hellier et al. (2014) | Andreasen et al. (2017) |
| WASP-47 | EPIC 206103150 | 22 04 48.731 | −12 01 07.99 |

|
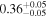
|
Hellier et al. (2012) | Mortier et al. (2013b) |
| HD 189733 | HD 189733 | 20 00 43.7128 | +22 42 39.074 |
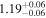
|
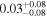
|
Bouchy et al. (2005) | Mortier et al. (2013b) |
| WASP-4 | 2MASS J23341508-4203411 | 23 34 15.082 | −42 03 41.14 |

|
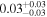
|
Wilson et al. (2008) | Mortier et al. (2013b) |
| TrES-2 | Kepler-1b | 19 07 14.035 | +49 18 59.07 |
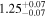
|
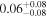
|
O'Donovan et al. (2006) | Ammler-von Eiff et al. (2009) |
| OGLE-TR-113 | V* V752 Car | 10 52 24.40 | −61 26 48.5 |
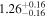
|
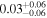
|
Bouchy et al. (2004) | Mortier et al. (2013b) |
| WASP-97 | CD-56 324 | 01 38 25.0569 | −55 46 19.511 |

|
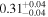
|
Hellier et al. (2014) | Andreasen et al. (2017) |
| WASP-12 | WASP-12 | 06 30 32.7943 | +29 40 20.287 |
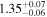
|
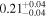
|
Hebb et al. (2009) | Mortier et al. (2013b) |
| HAT-P-8 | HAT-P-8 | 22 52 09.8629 | +35 26 49.605 |
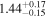
|
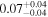
|
Latham et al. (2009) | Mortier et al. (2013b) |
| OGLE-TR-056 | V* V5157 Sgr | 17 56 35.51 | −29 32 21.2 |

|
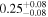
|
Konacki et al. (2003) | Santos et al. (2006) |
| WASP-72 | CD-30 1019 | 02 44 09.6110 | −30 10 08.570 |
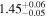
|
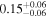
|
Gillon et al. (2013) | Andreasen et al. (2017) |
| WASP-50 | TYC 5290-462-1 | 02 54 45.1351 | −10 53 53.037 |
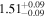
|
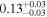
|
Gillon et al. (2011) | Mortier et al. (2013b) |
| KOI-1257 | Kepler-420 | 19 24 54.043 | +44 55 38.58 |

|
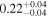
|
Santerne et al. (2014) | Santerne et al. (2014) |
| WASP-5 | GSC 08018-00199 | 23 57 23.759 | −41 16 37.74 |
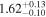
|
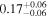
|
Anderson et al. (2008) | Mortier et al. (2013b) |
| WASP-77 A | BD-07 436A | 02 28 37.2266 | −07 03 38.366 |
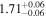
|
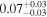
|
Maxted et al. (2013) | Mortier et al. (2013b) |
| K2-34 | TYC 1391-121-1 | 08 30 18.9080 | +22 14 09.313 |

|

|
Hirano et al. (2016) | Lillo-Box et al. (2016) |
| HAT-P-7 | BD+47 2846 | 19 28 59.3534 | +47 58 10.229 |

|

|
Pál et al. (2008) | Ammler-von Eiff et al. (2009) |
| TrES-3 | NAME TrES-3b | 17 52 07.020 | +37 32 46.18 |
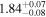
|
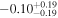
|
O'Donovan et al. (2007) | Ammler-von Eiff et al. (2009) |
| WASP-100 | CPD-64 356 | 04 35 50.3297 | −64 01 37.316 |

|
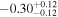
|
Hellier et al. (2014) | Andreasen et al. (2017) |
| WASP-73 | HD 202678 | 21 19 47.9070 | −58 08 55.951 |
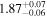
|
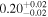
|
Delrez et al. (2014) | Andreasen et al. (2017) |
| WASP-3 | TYC 2636-195-1 | 18 34 31.6241 | +35 39 41.488 |
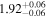
|
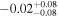
|
Pollacco et al. (2008) | Montalto et al. (2012) |
| WASP-37 | GSC 00326-00658 | 14 47 46.560 | +01 03 53.85 |
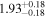
|

|
Simpson et al. (2011) | Andreasen et al. (2017) |
| HATS-1 | HATS-1 | 11 42 06.080 | −23 21 17.44 |
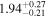
|
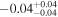
|
Penev et al. (2013) | Andreasen et al. (2017) |
| WASP-61 | TYC 6469-1972-1 | 05 01 11.9193 | −26 03 14.973 |

|

|
Hellier et al. (2012) | Andreasen et al. (2017) |
| HAT-P-23 | TYC 1632-1396-1 | 20 24 29.7254 | +16 45 43.812 |
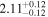
|
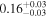
|
Bakos et al. (2011) | Tsantaki et al. (2014) |
| WASP-71 | TYC 30-116-1 | 01 57 03.2070 | +00 45 31.865 |

|
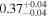
|
Smith et al. (2013) | Mortier et al. (2013b) |
| HAT-P-14 | TYC 3086-152-1 | 17 20 27.8775 | +38 14 31.911 |
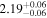
|
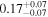
|
Torres et al. (2010) | Sousa et al. (2015) |
| WASP-36 | GSC 05442-00759 | 08 46 19.298 | −08 01 37.01 |
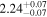
|
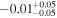
|
Smith et al. (2012) | Mortier et al. (2013b) |
| Kepler-17 | KOI-203 | 19 53 34.866 | +47 48 54.02 |
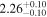
|
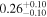
|
Désert et al. (2011) | Bonomo et al. (2012) |
| WASP-8 | TYC 7522-505-1 | 23 59 36.0711 | −35 01 52.920 |
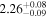
|
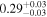
|
Queloz et al. (2010) | Mortier et al. (2013b) |
| HAT-P-22 | HD 233731 | 10 22 43.5927 | +50 07 42.060 |
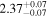
|
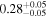
|
Bakos et al. (2011) | Sousa et al. (2015) |
| WASP-66 | TYC 7193-1804-1 | 10 32 53.9926 | −34 59 23.452 |
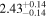
|
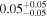
|
Hellier et al. (2012) | Mortier et al. (2013b) |
| WASP-99 | CD-50 777 | 02 39 35.4435 | −50 00 28.875 |
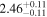
|
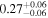
|
Hellier et al. (2014) | Andreasen et al. (2017) |
| CoRoT-10 | CoRoT-10 | 19 24 15.296 | +00 44 45.99 |
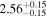
|
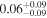
|
Bonomo et al. (2010) | Mortier et al. (2013b) |
| WASP-38 | HD 146389 | 16 15 50.3646 | +10 01 57.280 |
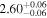
|

|
Barros et al. (2011) | Mortier et al. (2013b) |
| CoRoT-11 | CoRoT-11 | 18 42 44.947 | +05 56 15.70 |
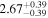
|
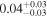
|
Gandolfi et al. (2010) | Tsantaki et al. (2014) |
| Qatar-2 | Qatar 2 | 13 50 37.409 | −06 48 14.41 |
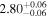
|

|
Bryan et al. (2012) | Andreasen et al. (2017) |
| Kepler-43 | Kepler-43 | 19 00 57.810 | +46 40 05.62 |
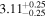
|
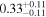
|
Bonomo et al. (2012) | Bonomo et al. (2012) |
| HD 17156 | HD 17156 | 02 49 44.4873 | +71 45 11.630 |

|
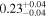
|
Fischer et al. (2007) | Ammler-von Eiff et al. (2009) |
| WASP-10 | GSC 02752-00114 | 23 15 58.299 | +31 27 46.28 |
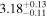
|
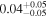
|
Christian et al. (2009) | Mortier et al. (2013b) |
| HAT-P-34 | HD 351766 | 20 12 46.8851 | +18 06 17.431 |

|
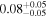
|
Bakos et al. (2012) | Tsantaki et al. (2014) |
| CoRoT-2 | CoRoT-2 | 19 27 06.496 | +01 23 01.38 |

|
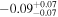
|
Alonso et al. (2008) | Mortier et al. (2013b) |
| WASP-32 | TYC 2-1155-1 | 00 15 50.8103 | +01 12 01.592 |
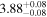
|
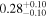
|
Maxted et al. (2010a) | Mortier et al. (2013b) |
| HD 80606 | HD 80606 | 09 22 37.5769 | +50 36 13.430 |

|
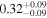
|
Naef et al. (2001) | Santos et al. (2004) |
| HAT-P-20 | HAT-P-20 | 07 27 39.950 | +24 20 11.49 |
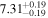
|

|
Bakos et al. (2011) | Mortier et al. (2013b) |
| HAT-P-2 | HD 147506 | 16 20 36.3576 | +41 02 53.107 |
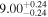
|
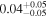
|
Bakos et al. (2007a) | Tsantaki et al. (2014) |
| WASP-18 | HD 10069 | 01 37 25.0332 | −45 40 40.373 |

|
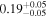
|
Hellier et al. (2009a) | Mortier et al. (2013b) |
| XO-3 | TYC 3727-1064-1 | 04 21 52.7053 | +57 49 01.868 |
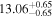
|

|
Johns-Krull et al. (2008) | Tsantaki et al. (2014) |
| CoRoT-3 | CoRoT-3 | 19 28 13.265 | +00 07 18.62 |
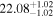
|

|
Deleuil et al. (2008) | Tsantaki et al. (2014) |
I compile from the literature a sample of brown dwarf and low-mass star secondaries with  that have Doppler-inferred masses and that transit solar-type dwarf primaries. I include in Table 2 the secondary masses and primary metallicities of the resulting sample of 27 systems. Because of the transit requirement, 95% of the objects in Table 2 have
that have Doppler-inferred masses and that transit solar-type dwarf primaries. I include in Table 2 the secondary masses and primary metallicities of the resulting sample of 27 systems. Because of the transit requirement, 95% of the objects in Table 2 have 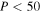 days and therefore
days and therefore 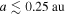 . This combined sample of 146 giant planets, brown dwarfs, and low-mass stars that have Doppler-inferred masses and transit solar-type primaries (most with homogeneously derived stellar parameters) is the best sample available to calculate the mass at which low-mass secondary companions no longer preferentially orbit metal-rich solar-type primaries.
. This combined sample of 146 giant planets, brown dwarfs, and low-mass stars that have Doppler-inferred masses and transit solar-type primaries (most with homogeneously derived stellar parameters) is the best sample available to calculate the mass at which low-mass secondary companions no longer preferentially orbit metal-rich solar-type primaries.
Table 2. Brown Dwarfs and Low-mass Stars that have Doppler-inferred Masses and Transit Solar-type Stars
| System | Simbad | R.A. | Decl. | Mass | Metallicity | Discovery | Parameter |
|---|---|---|---|---|---|---|---|
| Name | Reference | Referencea | |||||
| (h m s) | (d m s) | (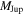 ) ) |
|||||
| Kepler-39 | KOI-423 | 19 47 50.468 | +46 02 03.43 |
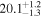
|
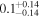
|
Bouchy et al. (2011a) | Bonomo et al. (2015) |
| KELT-1 | TYC 2785-2130-1 | 00 01 26.9206 | +39 23 01.773 |
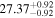
|
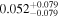
|
Siverd et al. (2012) | ⋯ |
| EPIC 219388192 | UCAC4 366-166973 | 19 17 34.026 | −16 52 17.75 |
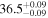
|
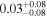
|
Curtis et al. (2016) | Nowak et al. (2017) |
| KOI-205 | KOI-205 | 19 41 59.197 | +42 32 16.40 |
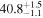
|
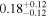
|
Díaz et al. (2013) | Bonomo et al. (2015) |
| CoRoT-33 | 2MASS J18383391+0537287 | 18 38 33.917 | +05 37 28.77 |
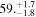
|
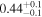
|
Csizmadia et al. (2015) | ⋯ |
| KOI-415 | KOI-415 | 19 33 13.452 | +41 36 22.94 |
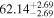
|
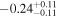
|
Moutou et al. (2013) | ⋯ |
| WASP-30 | WASP-30 | 23 53 38.0552 | −10 07 05.107 |
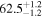
|
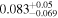
|
Anderson et al. (2011a) | Triaud et al. (2013) |
| CoRoT-15 | CoRoT-15 | 06 28 27.819 | +06 11 10.54 |

|

|
Bouchy et al. (2011b) | ⋯ |
| EPIC 201702477 | UCAC2 33047398 | 11 40 57.792 | +03 40 53.70 |
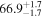
|
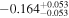
|
Bayliss et al. (2017) | ⋯ |
| KOI-189 | KOI-189 | 18 59 31.191 | +49 16 01.18 |
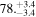
|
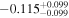
|
Díaz et al. (2014) | ⋯ |
| EBLM J0555-57A | CD-57 1311 | 05 55 32.6868 | −57 17 26.064 |
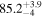
|
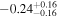
|
von Boetticher et al. (2017) | ⋯ |
| TYC 7760-484-1 | CD-39 7570 | 12 19 21.0385 | −39 51 25.575 |
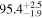
|

|
Triaud et al. (2013) | ⋯ |
| OGLE-TR-122 | V* V817 Car | 11 06 51.89 | −60 51 45.9 |

|
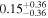
|
Pont et al. (2005) | ⋯ |
| 1SWASPJ234318.41+295556.5 | BD+29 4980 | 23 43 18.4125 | +29 55 56.696 |
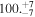
|
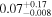
|
Chaturvedi et al. (2016) | ⋯ |
| CoRoT 101186644 | 2MASS J19265907+0029061 | 19 26 59.078 | +00 29 06.19 |

|
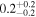
|
Tal-Or et al. (2013) | ⋯ |
| KOI-686 | KOI-686 | 19 47 21.783 | +43 38 49.64 |
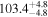
|
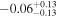
|
Díaz et al. (2014) | ⋯ |
| HATS550-016 | GSC 06465-00602 | 04 48 23.318 | −24 50 16.88 |
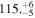
|
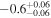
|
Zhou et al. (2014) | ⋯ |
| HAT-TR-205-013 | NAME HAT-TR-205-013 | 23 08 08.3420 | +33 38 03.963 |
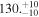
|

|
Beatty et al. (2007) | ⋯ |
| HATS551-021 | GSC 06493-00315 | 05 42 49.120 | −25 59 47.49 |
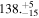
|
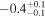
|
Zhou et al. (2014) | ⋯ |
| KIC 1571511 | KOI-362 | 19 23 59.256 | +37 11 57.19 |
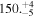
|
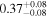
|
Ofir et al. (2012) | ⋯ |
| HATS551-019 | TYC 6493-290-1 | 05 40 46.1695 | −24 55 35.189 |
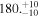
|
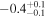
|
Zhou et al. (2014) | ⋯ |
| TYC 3700-1739-1 | TYC 3700-1739-1 | 02 40 51.519 | +52 45 06.27 |
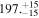
|
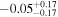
|
Eigmüller et al. (2016) | ⋯ |
| T-Lyr1-01662 | TYC 3545-371-1 | 18 59 02.8586 | +48 36 35.557 |
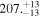
|

|
Fernandez et al. (2009) | ⋯ |
| HATS553-001 | GSC 05946-00892 | 06 16 00.656 | −21 15 23.82 |
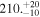
|
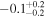
|
Zhou et al. (2014) | ⋯ |
| Kepler-16 | Kepler-16 | 19 16 18.175 | +51 45 26.76 |

|
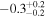
|
Doyle et al. (2011) | ⋯ |
| T-Lyr0-08070 | TYC 3121-1659-1 | 19 19 03.7120 | +38 40 56.775 |
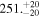
|
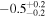
|
Fernandez et al. (2009) | ⋯ |
| HD 213572 | HD 213572 | 22 32 00.1305 | +27 14 09.767 |

|
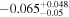
|
Chaturvedi et al. (2014) | ⋯ |
Note.
aOnly included if it is different than the discovery reference.Download table as: ASCIITypeset image
Selection effects are unlikely to be present in this sample. In a signal-to-noise limited transit survey at a given period the number of systems discovered, N, scales as 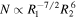 , where R1 is primary radius and R2 is the secondary radius (Pepper et al. 2003). All of the brown dwarfs and low-mass stars as well as almost all of the giant planets in this sample were discovered with the transit technique. They all orbit solar-type host stars with similar radii, so
, where R1 is primary radius and R2 is the secondary radius (Pepper et al. 2003). All of the brown dwarfs and low-mass stars as well as almost all of the giant planets in this sample were discovered with the transit technique. They all orbit solar-type host stars with similar radii, so  for all 146 systems in the sample considered here. Because giant planets and brown dwarfs are both significantly supported by degeneracy pressure, radius is a weak function of mass in the interval of
for all 146 systems in the sample considered here. Because giant planets and brown dwarfs are both significantly supported by degeneracy pressure, radius is a weak function of mass in the interval of 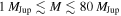 (e.g., Zapolsky & Salpeter 1969; Burrows & Liebert 1993). Consequently, all 146 systems in this sample have
(e.g., Zapolsky & Salpeter 1969; Burrows & Liebert 1993). Consequently, all 146 systems in this sample have 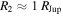 . The Doppler technique can easily detect the orbital motion of the primary in all 146 systems in this sample, so it can be used to estimate the mass of the secondary in each system. For these reasons, transit surveys are equally complete for objects across the mass range of this sample.
. The Doppler technique can easily detect the orbital motion of the primary in all 146 systems in this sample, so it can be used to estimate the mass of the secondary in each system. For these reasons, transit surveys are equally complete for objects across the mass range of this sample.
Even though the period distribution of the transiting secondaries in this sample is biased toward short periods, that bias will not affect my goal of calculating the mass at which secondary companions no longer preferentially orbit metal-rich solar-type dwarf primaries. Both the preference of giant planets for metal-rich primaries and the indifference of low-mass stars to primary metallicity are independent of the period: Fischer & Valenti (2005) showed that giant planets preferentially orbit metal-rich stars at all periods while Latham et al. (2002) demonstrated that the occurrence and period distributions of metal-poor and metal-rich binary systems are indistinguishable. Accordingly, there is no reason to believe that a similar analysis on a sample of the more common intermediate-period secondaries would produce a qualitatively different conclusion.
3. Analysis
With the goal of identifying the mass at which low-mass secondaries no longer preferentially orbit solar-type dwarf primaries, I analyze the 146 systems in Tables 1 and 2 in two independent ways. First, I apply clustering algorithms to the data in the log10(secondary mass)–primary metallicity plane. Since each secondary formed either through core accretion or gravitational instability, I specify in advance that each algorithm should put each secondary in one of two clusters. The mass that forms the border between the two clusters is the mass at which secondaries no longer preferentially occur around metal-rich solar-type dwarf stars, which I interpret as the maximum mass of celestial bodies that form like planets through core accretion. Second, I take advantage of the theoretical prediction of Mordasini et al. (2012) that massive objects formed by core accretion should only occur around the most metal-rich primaries. To that end, I calculate the median metallicity of the sample as a function of secondary mass in a kernel of constant width. I interpret the point at which the moving median metallicity drops below the smallest value seen in the planet mass range as the maximum mass of objects that form like planets, as massive objects formed by core accretion should orbit stars more metal-rich than that of the typical giant planet–host star. I detail these analyses in the following two subsections. I then use a semi-analytic model of the runaway gas accretion stage of giant planet formation to interpret the results in the last subsection.
3.1. Clustering Analysis
I use clustering algorithms from each of three classical clustering paradigms that span the space of modern clustering approaches: connectivity-based hierarchical clustering (Murtagh 1985), centroid-based k-means clustering (Hartigan & Wong 1979), and distribution-based Gaussian-model clustering (Fraley & Raftery 2002; Fraley et al. 2012; Schlaufman 2015). I summarize the key aspects of each algorithm below and provide the details in Appendix B.
The hierarchical clustering algorithm seeks to identify the maximally connected subgraph of a set of objects. It starts with a matrix of dissimilarity between all objects in a set. It then identifies the pair of objects with the smallest dissimilarity, combines them, and updates the dissimilarity of all remaining objects in the set with the minimum dissimilarity to either of the combined objects. It continues this process until only two objects remain. This algorithm requires the specification of a dissimilarity metric, and I use the Euclidean distance between each object.
The k-means clustering algorithm seeks to minimize the total dissimilarity between the ensemble of objects in each cluster and the cluster center. It starts by randomly placing a set of cluster centers in the space defined by the objects to be clustered. It then identifies the closest cluster center to each object and assigns that object to that cluster. The mean value of the ensemble of objects in each cluster is then set to be that cluster's center on the next iteration. The process continues until the movement of cluster centers on each update step is small. This algorithm requires the specification of a dissimilarity metric, and I use the Euclidean distance between each object.
The Gaussian-model clustering algorithm seeks to identify the mixture of Gaussians that has the highest likelihood of having generated the objects to be clustered. It starts by randomly choosing the mean and variance of each Gaussian as well as the contribution of each Gaussian to the mixture. It then calculates the probability that each observation was produced by one component of the mixture. The object is assigned to the component most likely to have generated it and the mean and variance of each component are estimated based on the objects assigned to it. The proportion of each component is the fraction of objects assigned to it. This process is repeated until the change in model parameters is small.
To account for the observational uncertainty in each secondary mass and primary metallicity, I use a Monte Carlo simulation. First, I generate 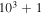 realizations of each secondary mass and primary metallicity from the observational uncertainties on those quantities and then apply all three clustering algorithms to each realization. For each algorithm, I aggregate the classifications across all iterations and assign to each system the most frequently determined classification. The final classification of each system is then the majority classification among the three different algorithms. I plot the result of this calculation in Figure 1. All systems with a secondary mass of
realizations of each secondary mass and primary metallicity from the observational uncertainties on those quantities and then apply all three clustering algorithms to each realization. For each algorithm, I aggregate the classifications across all iterations and assign to each system the most frequently determined classification. The final classification of each system is then the majority classification among the three different algorithms. I plot the result of this calculation in Figure 1. All systems with a secondary mass of 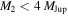 are unanimously classified with giant planets, while all systems with a secondary mass of
are unanimously classified with giant planets, while all systems with a secondary mass of 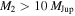 are unanimously classified with low-mass stars. A two-sample Kolmogorov–Smirnov test on the overall sample split at
are unanimously classified with low-mass stars. A two-sample Kolmogorov–Smirnov test on the overall sample split at 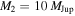 shows that the chance that the two metallicity distributions were produced by the same parent distribution is only
shows that the chance that the two metallicity distributions were produced by the same parent distribution is only 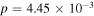 , or about
, or about  .1
.1
Figure 1. Secondary mass–primary metallicity distribution for giant planets, brown dwarfs, and low-mass stars that transit solar-type dwarf stars. Objects classified unanimously by all three of the clustering paradigms are plotted as solid symbols, with circles for planets and squares for low-mass stars. Objects with classes agreed upon by two of the three clustering paradigms are plotted as open symbols, with circles for planets and squares for low-mass stars. The gray shading separates the unanimous classification regions. The black dashed line is the midpoint of the gray region. The blue and green regions are the best-fit two-component Gaussian mixture model, while the black cross in the lower right corner of the plot indicates the typical uncertainty.
Download figure:
Standard image High-resolution image3.2. Moving Median Analysis
The clustering analysis described above implicitly makes use of the relative occurrence rates of giant planets, brown dwarfs, and low-mass stars. An alternative approach that does not implicitly use the occurrence rate is to calculate the median metallicity as a function of secondary mass in a kernel of a constant width. Since celestial bodies with 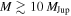 formed via core accretion are thought to occur only around the most metal-rich stars (Mordasini et al. 2012), the mass at which the moving median metallicity moves below the lowest moving median metallicity observed in the giant planet region should also correspond to the maximum mass of the objects formed by core accretion.
formed via core accretion are thought to occur only around the most metal-rich stars (Mordasini et al. 2012), the mass at which the moving median metallicity moves below the lowest moving median metallicity observed in the giant planet region should also correspond to the maximum mass of the objects formed by core accretion.
To account for the observational uncertainty in each secondary mass and primary metallicity, I use a Monte Carlo simulation. First, I generate 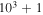 realizations of each secondary mass and primary metallicity from the observational uncertainties on those quantities and then calculate the moving median metallicity of each sample as a function of mass. I use a kernel of width n = 23 objects, as this is the highest mass resolution that permits the measurement of the median metallicity with a similar precision as for the individual metallicity estimates (
realizations of each secondary mass and primary metallicity from the observational uncertainties on those quantities and then calculate the moving median metallicity of each sample as a function of mass. I use a kernel of width n = 23 objects, as this is the highest mass resolution that permits the measurement of the median metallicity with a similar precision as for the individual metallicity estimates (![${\sigma }_{[\mathrm{Fe}/{\rm{H}}]}\approx 0.05$](https://content.cld.iop.org/journals/0004-637X/853/1/37/revision1/apjaa961cieqn335.gif) dex). I plot this result in Figure 2. Again, the point at which secondaries no longer preferentially orbit metal-rich solar-type dwarf-star primaries occurs at
dex). I plot this result in Figure 2. Again, the point at which secondaries no longer preferentially orbit metal-rich solar-type dwarf-star primaries occurs at 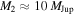 . This result is similar for all kernel widths that permit the measurement of the median metallicity with a similar precision as for the individual metallicity estimates.
. This result is similar for all kernel widths that permit the measurement of the median metallicity with a similar precision as for the individual metallicity estimates.
Figure 2. Moving median metallicity as a function of secondary mass. The black line is the median metallicity in a kernel of width n =23 centered on the given mass. The gray region is the 1σ uncertainty in the moving median. The blue rectangle indicates the range of median metallicity observed in the giant planet region. The green rectangle shows the range in mass where the moving median is below that seen in the giant planet region (i.e., 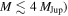 . The boundary is near
. The boundary is near  .
.
Download figure:
Standard image High-resolution image3.3. Parameter Study of the Last Stage of Giant Planet Formation
The results in Sections 3.1 and 3.2 show that low-mass secondaries no longer preferentially orbit metal-rich solar-type dwarf stars when 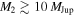 . Those inferences support the idea that the most massive objects formed around solar-type stars like planets through core accretion have
. Those inferences support the idea that the most massive objects formed around solar-type stars like planets through core accretion have 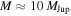 . I now use that inference to quantify the range of protoplanetary disk properties that could be expected to reproduce this result using the semi-analytic model of Tanigawa & Tanaka (2016).
. I now use that inference to quantify the range of protoplanetary disk properties that could be expected to reproduce this result using the semi-analytic model of Tanigawa & Tanaka (2016).
Tanigawa & Tanaka (2016) modeled the last stage of giant planet formation (runaway envelope accretion) in a globally evolving protoplanetary disk using the Shakura & Sunyaev (1973) model for disk viscosity and a self-similar solution for the disk's global evolution (e.g., Lynden-Bell & Pringle 1974; Hartmann et al. 1998). The key parameters of the model are as follows.
- 1.The location of planet formation, ap.
- 2.The disk viscosity,
 , where α is a unitless parameter independent of radius and time, c is the sound speed of disk gas, and h is the disk scale height.
, where α is a unitless parameter independent of radius and time, c is the sound speed of disk gas, and h is the disk scale height. - 3.The initial mass of the disk,
 , is assumed to scale linearly with a host star mass, M*, and overall normalization,
, is assumed to scale linearly with a host star mass, M*, and overall normalization,  . Here
. Here  corresponds to the minimum-mass solar nebula of Hayashi et al. (1985).
corresponds to the minimum-mass solar nebula of Hayashi et al. (1985). - 4.The characteristic exponential disk depletion time,
 .
.
The model is informed by the latest numerical results showing that gaps cleared by giant planets are much shallower than previously thought (e.g., Duffell & MacFadyen 2013; Fung et al. 2014). The model does not account for possible photoevaporation of disk gas due to far-ultraviolet radiation (e.g., Gorti et al. 2009), as the rate of mass loss expected is still uncertain by more than an order of magnitude (e.g., Alexander et al. 2014).
I have implemented the Tanigawa & Tanaka (2016) model and used it to conduct a parameter study of the relationship between the maximum attainable mass of a giant planet and the model parameters ap, α, M*, 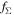 , and
, and 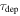 . If not otherwise indicated, I assume that ap = 1 au,
. If not otherwise indicated, I assume that ap = 1 au, 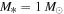 ,
,  , the initial disk radius is
, the initial disk radius is 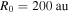 , and the seed embryo mass is
, and the seed embryo mass is  . I plot the result in Figure 3. According to the model, a maximum giant planet mass in the range of
. I plot the result in Figure 3. According to the model, a maximum giant planet mass in the range of 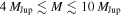 can be accommodated only in a narrow corridor of the α–
can be accommodated only in a narrow corridor of the α– plane from
plane from  and
and 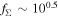 to
to 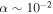 and
and  . This result is only weakly dependent on the mass of the primary star, the location of planet formation, or the disk depletion time. These results are unique in that they indirectly constrain the viscosities and masses of long since dissipated disks during their epoch of giant planet formation.
. This result is only weakly dependent on the mass of the primary star, the location of planet formation, or the disk depletion time. These results are unique in that they indirectly constrain the viscosities and masses of long since dissipated disks during their epoch of giant planet formation.
Figure 3. Maximum mass attainable by a giant planet formed by core accretion according the model of Tanigawa & Tanaka (2016) as a function of the viscosity parameter α of Shakura & Sunyaev (1973) and the minimum-mass solar nebular scaling factor, 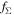 . Dark colors are indicative of high-mass planets, while lighter colors are indicative of low-mass planets. The labeled contours delimit the region of maximum mass permitted by the analyses presented in Sections 3.1 and 3.2. The top row varies the host star mass, M*, the middle row varies the location of planet formation, ap, and the bottom row varies the characteristic disk depletion time,
. Dark colors are indicative of high-mass planets, while lighter colors are indicative of low-mass planets. The labeled contours delimit the region of maximum mass permitted by the analyses presented in Sections 3.1 and 3.2. The top row varies the host star mass, M*, the middle row varies the location of planet formation, ap, and the bottom row varies the characteristic disk depletion time, 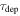 .
.
Download figure:
Standard image High-resolution image4. Discussion
I have shown that celestial bodies with  orbit metal-rich solar-type dwarf stars, a property thought to indicate formation through core accretion (e.g., Santos et al. 2004; Fischer & Valenti 2005). On the other hand, celestial bodies with
orbit metal-rich solar-type dwarf stars, a property thought to indicate formation through core accretion (e.g., Santos et al. 2004; Fischer & Valenti 2005). On the other hand, celestial bodies with  do not preferentially orbit metal-rich stars, so there is no reason to believe that they form through core accretion. Since gravitational instability is thought to be independent of metallicity (e.g., Boss 2002), it can easily accommodate this observation.
do not preferentially orbit metal-rich stars, so there is no reason to believe that they form through core accretion. Since gravitational instability is thought to be independent of metallicity (e.g., Boss 2002), it can easily accommodate this observation.
This boundary at 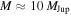 between objects formed via core accretion and gravitational instability is coincident with a minimum in the occurrence rate of companions to solar-type dwarf stars with
between objects formed via core accretion and gravitational instability is coincident with a minimum in the occurrence rate of companions to solar-type dwarf stars with  days as a function of minimum mass. I plot the occurrence rate of giant planets, brown dwarfs, and low-mass stars discovered with the Doppler technique in Figure 4. The observation that the upper limit on the mass of giant planets identified by the clustering analysis occurs at the minimum in the occurrence rate of celestial bodies orbiting solar-type dwarf stars supports the idea that core accretion does not generally form objects with
days as a function of minimum mass. I plot the occurrence rate of giant planets, brown dwarfs, and low-mass stars discovered with the Doppler technique in Figure 4. The observation that the upper limit on the mass of giant planets identified by the clustering analysis occurs at the minimum in the occurrence rate of celestial bodies orbiting solar-type dwarf stars supports the idea that core accretion does not generally form objects with 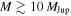 .
.
Figure 4. Secondary occurrence rate as a function of secondary minimum mass at  days. The secondary occurrence rate in the range of
days. The secondary occurrence rate in the range of 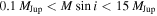 is from Cumming et al. (2008), while the occurrence rate in the range of
is from Cumming et al. (2008), while the occurrence rate in the range of 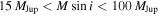 is from Troup et al. (2016). The gray shading and black dashed line are the same as in Figure 1. They separate the regions identified by the clustering analysis.
is from Troup et al. (2016). The gray shading and black dashed line are the same as in Figure 1. They separate the regions identified by the clustering analysis.
Download figure:
Standard image High-resolution imageThis boundary at 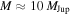 between objects formed via core accretion and gravitational instability is also supported by interior models for three massive objects that straddle the boundary: HAT-P-20 b (
between objects formed via core accretion and gravitational instability is also supported by interior models for three massive objects that straddle the boundary: HAT-P-20 b (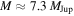 —Bakos et al. 2011), HAT-P-2 b (
—Bakos et al. 2011), HAT-P-2 b ( —Bakos et al. 2007a), and Kepler-75 b (
—Bakos et al. 2007a), and Kepler-75 b ( —Bonomo et al. 2015). Interior models indicate HAT-P-20 b and HAT-P-2 b have large amounts of heavy elements as expected if they formed through core accretion, while Kepler-75 b is consistent with the composition of its host star as expected if it formed through gravitational instability (Leconte et al. 2009; Thorngren et al. 2016).
—Bonomo et al. 2015). Interior models indicate HAT-P-20 b and HAT-P-2 b have large amounts of heavy elements as expected if they formed through core accretion, while Kepler-75 b is consistent with the composition of its host star as expected if it formed through gravitational instability (Leconte et al. 2009; Thorngren et al. 2016).
4.1. Implications for Planet Formation
The results presented in Section 3 indicate that a 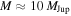 maximum mass for objects formed by core accretion can only be accommodated in a narrow band in the Shakura & Sunyaev (1973) viscosity parameter α–minimum-mass solar nebular scaling factor
maximum mass for objects formed by core accretion can only be accommodated in a narrow band in the Shakura & Sunyaev (1973) viscosity parameter α–minimum-mass solar nebular scaling factor 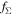 plane from
plane from  and
and 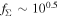 to
to 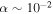 and
and  . Observations of T Tauri stars have been used to suggest that protoplanetary disks can be reproduced by models with
. Observations of T Tauri stars have been used to suggest that protoplanetary disks can be reproduced by models with 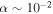 (e.g., Hartmann et al. 1998). At the same time, classical models of giant planet formation though core accretion almost always invoke disks several times more massive than that of the minimum-mass solar nebula—or
(e.g., Hartmann et al. 1998). At the same time, classical models of giant planet formation though core accretion almost always invoke disks several times more massive than that of the minimum-mass solar nebula—or 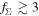 —to ensure core formation before disk dissipation (e.g., Pollack et al. 1996; Ikoma et al. 2000; Alibert et al. 2005; Hubickyj et al. 2005; Lissauer et al. 2009; Movshovitz et al. 2010; D'Angelo et al. 2014). In a disk with
—to ensure core formation before disk dissipation (e.g., Pollack et al. 1996; Ikoma et al. 2000; Alibert et al. 2005; Hubickyj et al. 2005; Lissauer et al. 2009; Movshovitz et al. 2010; D'Angelo et al. 2014). In a disk with  and
and 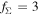 , the Tanigawa & Tanaka (2016) model predicts a giant planet maximum mass of
, the Tanigawa & Tanaka (2016) model predicts a giant planet maximum mass of 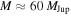 . According to these results, either but not both, of these traditional assumptions could be made during the runaway gas accretion stage of giant planet formation.
. According to these results, either but not both, of these traditional assumptions could be made during the runaway gas accretion stage of giant planet formation.
If the 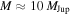 threshold is the result of low-viscosity or low-mass disks, then it would provide a solution to the long-standing Type I and Type II migration problems. Type I migration occurs when planetary embryos with
threshold is the result of low-viscosity or low-mass disks, then it would provide a solution to the long-standing Type I and Type II migration problems. Type I migration occurs when planetary embryos with 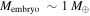 that are not massive enough to open a gap in their parent protoplanetary disks lose angular momentum and move inward due to net negative torques from the disk. Though the processes responsible are complex and no model is yet completely satisfactory, the simplest models suggest that the timescale for migration is very fast (e.g., Ward 1997; Tanaka et al. 2002). Exoplanet population synthesis calculations assuming fast Type I migration are unable to reproduce the existence of planets with
that are not massive enough to open a gap in their parent protoplanetary disks lose angular momentum and move inward due to net negative torques from the disk. Though the processes responsible are complex and no model is yet completely satisfactory, the simplest models suggest that the timescale for migration is very fast (e.g., Ward 1997; Tanaka et al. 2002). Exoplanet population synthesis calculations assuming fast Type I migration are unable to reproduce the existence of planets with 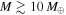 and
and 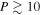 days, so Type I migration must be slower than the simplest calculations initially suggested (e.g., Ida & Lin 2008; Schlaufman et al. 2009). While many solutions have been proposed,2
it has been shown that Type I migration in disks with
days, so Type I migration must be slower than the simplest calculations initially suggested (e.g., Ida & Lin 2008; Schlaufman et al. 2009). While many solutions have been proposed,2
it has been shown that Type I migration in disks with 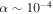 is sufficiently slow that planetary embryos will survive and potentially grow into giant planets (e.g., Rafikov 2002; Li et al. 2009). Similarly, in disks with
is sufficiently slow that planetary embryos will survive and potentially grow into giant planets (e.g., Rafikov 2002; Li et al. 2009). Similarly, in disks with 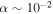 , the Type I migration rate is thought to be linearly dependent on disk surface density (e.g., Baruteau et al. 2016). A minimum-mass solar nebular scaling factor of
, the Type I migration rate is thought to be linearly dependent on disk surface density (e.g., Baruteau et al. 2016). A minimum-mass solar nebular scaling factor of 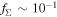 would reduce the Type I migration rate by an order of magnitude, exactly the amount needed to reproduce the observed distribution of exoplanet properties in population synthesis calculations (e.g., Ida & Lin 2008; Schlaufman et al. 2009).
would reduce the Type I migration rate by an order of magnitude, exactly the amount needed to reproduce the observed distribution of exoplanet properties in population synthesis calculations (e.g., Ida & Lin 2008; Schlaufman et al. 2009).
Low-viscosity or low-mass disks would also solve the Type II migration problem. Type II migration occurs when planets that are massive enough to open a gap in their parent protoplanetary disks are carried into the close proximity of their host star on the disk viscous time (Lin et al. 1996), possibly precluding the existence of long-period giant planets. In disks where the mass of the disk locally dominates the mass of the planet, the Type II migration rate is inversely proportional to the viscosity (e.g., Lin et al. 1996; Tanigawa & Tanaka 2016). Similarly, in a low-mass disk where the mass of the planet locally dominates the mass of the disk, the Type II migration rate is inversely proportional to the disk mass (e.g., Duffell et al. 2014). Consequently, low-viscosity or low-mass disks promote the existence of long-period giant planets.
Though these results were derived strictly for solar-type dwarf stars with short-period transiting companions, the analysis in Section 3.3 suggests that the inference about planet formation is not strongly dependent on host-star mass, planet-formation location, or disk dissipation timescale. Indeed, similar inferences have been made using the much-more distant solar system giant planets Jupiter and Saturn by Lissauer et al. (2009) and Tanigawa & Tanaka (2016). It is also reassuring that this upper limit of 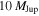 on the mass of planets within 1 au of their host stars is consistent with the most advanced exoplanet population synthesis calculations currently available (Ida et al. 2013). Finally, support for low-viscosity or low-mass disks as the origin of planetary systems has been found in many places from meteoritics in the solar system to super-Earths and mini-Neptunes in the Kepler field (e.g., Desch et al. 2017; Lee et al. 2017).
on the mass of planets within 1 au of their host stars is consistent with the most advanced exoplanet population synthesis calculations currently available (Ida et al. 2013). Finally, support for low-viscosity or low-mass disks as the origin of planetary systems has been found in many places from meteoritics in the solar system to super-Earths and mini-Neptunes in the Kepler field (e.g., Desch et al. 2017; Lee et al. 2017).
4.2. Comparison to Previous Studies of the Relationship between Giant Planets, Brown Dwarfs, and Host-star Properties
This study focused on giant planets, brown dwarfs, and low-mass stars with Doppler-inferred masses transiting solar-type dwarf stars with homogeneously estimated stellar parameters. It showed that low-mass secondaries with 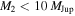 preferentially orbit metal-rich stars, while secondaries with
preferentially orbit metal-rich stars, while secondaries with 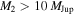 occur independent of host star metallicity. The difference between the metallicity distributions of objects in my sample with
occur independent of host star metallicity. The difference between the metallicity distributions of objects in my sample with 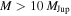 and
and 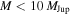 is significant at more than
is significant at more than  , and this result cannot be attributed solely to the possible change in the occurrence rate of such bodies at
, and this result cannot be attributed solely to the possible change in the occurrence rate of such bodies at 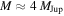 . Since a preference for metal-rich host stars is thought to indicate formation through core accretion, these results suggest that the most massive objects that can be formed like planets through core accretion have
. Since a preference for metal-rich host stars is thought to indicate formation through core accretion, these results suggest that the most massive objects that can be formed like planets through core accretion have  .
.
Unlike all previous studies, these results are unaffected by the Doppler  degeneracy, the presence of possible false positives in the analysis sample, or the potentially weak or nonexistent giant planet–host star metallicity correlation for giant stars (e.g., Sadakane et al. 2005; Schuler et al. 2005; Hekker & Meléndez 2007; Pasquini et al. 2007; Takeda et al. 2008; Ghezzi et al. 2010; Maldonado et al. 2013; Mortier et al. 2013a; Jofré et al. 2015; Reffert et al. 2015). Because of its large sample and use of M instead of
degeneracy, the presence of possible false positives in the analysis sample, or the potentially weak or nonexistent giant planet–host star metallicity correlation for giant stars (e.g., Sadakane et al. 2005; Schuler et al. 2005; Hekker & Meléndez 2007; Pasquini et al. 2007; Takeda et al. 2008; Ghezzi et al. 2010; Maldonado et al. 2013; Mortier et al. 2013a; Jofré et al. 2015; Reffert et al. 2015). Because of its large sample and use of M instead of  , it has the best resolution in mass of all studies to date. All of these properties have enabled the identification of a difference between the metallicity distributions of objects with
, it has the best resolution in mass of all studies to date. All of these properties have enabled the identification of a difference between the metallicity distributions of objects with 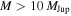 and
and  at a higher statistical significance than any previous study of solar-type dwarfs. It is also the first study to couple its result to a detailed model of the runaway gas accretion stage of giant planet formation to constrain the properties of protoplanetary disks that are known to have formed giant planets.
at a higher statistical significance than any previous study of solar-type dwarfs. It is also the first study to couple its result to a detailed model of the runaway gas accretion stage of giant planet formation to constrain the properties of protoplanetary disks that are known to have formed giant planets.
The first studies seeking to compare giant planets and brown dwarfs to explore their origin all focused on the orbital properties of brown dwarfs. Grether & Lineweaver (2006) examined the mass distribution of companions to solar-type stars with 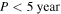 and determined that the minimum of the distribution occurs at
and determined that the minimum of the distribution occurs at 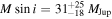 . Because there was no such minimum in the mass spectrum of free-floating brown dwarfs, they speculated that migration and not a characteristic mass scale of fragmentation in protoplanetary disks was responsible for the apparent minimum.
. Because there was no such minimum in the mass spectrum of free-floating brown dwarfs, they speculated that migration and not a characteristic mass scale of fragmentation in protoplanetary disks was responsible for the apparent minimum.
Sahlmann et al. (2011) used the combination of the Doppler and astrometric techniques to remove the 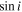 degeneracy to confirm the previous result, finding that low-mass brown dwarfs with
degeneracy to confirm the previous result, finding that low-mass brown dwarfs with 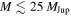 cleanly separated from high-mass brown dwarfs with
cleanly separated from high-mass brown dwarfs with  . In contrast to Grether & Lineweaver (2006), they argued that the low-mass brown dwarfs may be massive planets formed by core accretion. They also showed that samples of brown dwarf candidates discovered solely by the Doppler technique with
. In contrast to Grether & Lineweaver (2006), they argued that the low-mass brown dwarfs may be massive planets formed by core accretion. They also showed that samples of brown dwarf candidates discovered solely by the Doppler technique with  are significantly contaminated by inclined low-mass stars.3
are significantly contaminated by inclined low-mass stars.3
Ma & Ge (2014) extended these results by demonstrating that brown dwarfs with 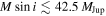 and
and 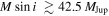 are unlikely to have the same eccentricity distribution at the 2.1σ level. They suggested that the low-mass brown dwarfs formed by disk fragmentation, while the high-mass brown dwarfs formed by fragmentation at the core scale. They also showed that the giant planet and brown dwarf host stars were unlikely to have the same metallicity distribution at the 3.3σ level. Selection effects in the giant planet–host sample and inclined low-mass star contamination in the brown dwarf sample likely affect these conclusions to some degree though.
are unlikely to have the same eccentricity distribution at the 2.1σ level. They suggested that the low-mass brown dwarfs formed by disk fragmentation, while the high-mass brown dwarfs formed by fragmentation at the core scale. They also showed that the giant planet and brown dwarf host stars were unlikely to have the same metallicity distribution at the 3.3σ level. Selection effects in the giant planet–host sample and inclined low-mass star contamination in the brown dwarf sample likely affect these conclusions to some degree though.
More recent efforts to investigate the differences between massive planets and brown dwarfs have focused on host star metallicity and chemical abundance. Using a sample of solar-type dwarf stars unaffected by selection effects or inclined low-mass star contamination, Mata Sánchez et al. (2014) found that the metallicities and α-element abundances of brown dwarf hosts are lower than the metallicities of giant planet–host stars at the 1.7σ and 1.8σ levels.
Maldonado & Villaver (2017) presented a similar analysis to Ma & Ge (2014) that used homogeneously derived stellar parameters to show that low-mass brown dwarf hosts are more metal-rich than high-mass brown dwarf hosts at the 2.4σ level. However, the difference was not significant if only dwarf host stars were included or if a random distribution of inclination was assumed. The fact that the significance of their result is reduced when accounting for a random distribution of inclination suggests that low-mass stars on low-inclination orbits contaminated their sample. In addition, their compete sample of brown dwarf hosts was significantly more metal-poor than their sample of giant planet–host stars. At the same time, their low-mass brown dwarfs were consistent with having the same metallicity distribution as the giant planet–host stars, though their α-element distributions differed at the 2.4σ level.
Santos et al. (2017) studied the minimum-mass and metallicity distributions of mostly Doppler-discovered objects with 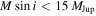 ,
, 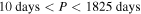 , and with homogeneous stellar parameters available in the SWEET-Cat database. Using both multivariate Gaussian modeling and Kolmogorov–Smirnov tests, they argued that planets below and above
, and with homogeneous stellar parameters available in the SWEET-Cat database. Using both multivariate Gaussian modeling and Kolmogorov–Smirnov tests, they argued that planets below and above 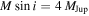 have distinct metallicity distributions and therefore distinct formation channels. In particular, they suggested that the giant planets with
have distinct metallicity distributions and therefore distinct formation channels. In particular, they suggested that the giant planets with 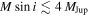 formed via core accretion while the giant planets with
formed via core accretion while the giant planets with 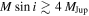 formed via gravitational instability. Their multivariate Gaussian inference is mostly due to the apparent cutoff in the giant planet occurrence distribution at
formed via gravitational instability. Their multivariate Gaussian inference is mostly due to the apparent cutoff in the giant planet occurrence distribution at 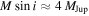 . In their Kolmogorov–Smirnov tests, the distributions were distinct at the 3.3σ significance substantially because of the inclusion of giant stars with
. In their Kolmogorov–Smirnov tests, the distributions were distinct at the 3.3σ significance substantially because of the inclusion of giant stars with  . The fact that restricting the sample to solar-type dwarf stars reduced the significance of their inference to 1.6σ indicates that either false positives in the giant star sample or the possibly diminished giant planet occurrence–host star metallicity effect for giant stars may play a role in the significant difference they identified in their sample including both dwarf and giant host stars. A critical mass of
. The fact that restricting the sample to solar-type dwarf stars reduced the significance of their inference to 1.6σ indicates that either false positives in the giant star sample or the possibly diminished giant planet occurrence–host star metallicity effect for giant stars may play a role in the significant difference they identified in their sample including both dwarf and giant host stars. A critical mass of 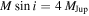 is also inconsistent with the heavy element enrichment observed in HAT-P-20 b and HAT-P-2 b. Nevertheless, my study confirms the hint identified in Santos et al. (2017) and presents the strongest evidence to date that the maximum mass of objects formed via core accretion is in the range of
is also inconsistent with the heavy element enrichment observed in HAT-P-20 b and HAT-P-2 b. Nevertheless, my study confirms the hint identified in Santos et al. (2017) and presents the strongest evidence to date that the maximum mass of objects formed via core accretion is in the range of 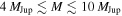 .
.
4.3. A Formation-based Definition for Planets
This analysis has shown that objects with 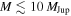 preferentially orbit metal-rich solar-type dwarf stars. That property has been suggested to be a natural outcome of the core accretion model of giant planet formation. On the other hand, objects with
preferentially orbit metal-rich solar-type dwarf stars. That property has been suggested to be a natural outcome of the core accretion model of giant planet formation. On the other hand, objects with 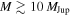 orbit stars spanning the whole range of the thin disk metallicity distribution. That property is shared with low-mass stars, which must have formed by some sort of gravitational instability.
orbit stars spanning the whole range of the thin disk metallicity distribution. That property is shared with low-mass stars, which must have formed by some sort of gravitational instability.
I propose that planets be defined as objects that orbit stars or stellar remnants and have a true mass below the threshold at which low-mass companions no longer preferentially orbit metal-rich solar-type dwarf stars. The analyses presented in Sections 3.1 and 3.2 suggest this threshold is at 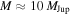 , but future data may revise this estimate. This definition has the same form as the working definition adopted by the IAU Working Group on Extrasolar Planets, but the maximum mass is now referenced to the maximum mass of objects formed by core accretion. This definition does not require the specification of an arbitrarily amount of deuterium burning, and it does not depend on an object's metallicity. Additionally, it is independent of the uncertain internal structure of objects at this mass scale. Furthermore, I propose that substellar objects with true masses above the threshold be defined as brown dwarfs, regardless of where they are located.
, but future data may revise this estimate. This definition has the same form as the working definition adopted by the IAU Working Group on Extrasolar Planets, but the maximum mass is now referenced to the maximum mass of objects formed by core accretion. This definition does not require the specification of an arbitrarily amount of deuterium burning, and it does not depend on an object's metallicity. Additionally, it is independent of the uncertain internal structure of objects at this mass scale. Furthermore, I propose that substellar objects with true masses above the threshold be defined as brown dwarfs, regardless of where they are located.
4.4. Predictions for Future Gaia Observations
The results presented in Sections 3.1 and 3.2 lead to the prediction that planets with  should preferentially be found around metal-rich solar-type dwarf stars. In contrast, brown dwarfs with
should preferentially be found around metal-rich solar-type dwarf stars. In contrast, brown dwarfs with  should be found around solar-type dwarf stars that span the metallicity range of the Milky Way's thin disk. This prediction will soon be tested at an unprecedented scale. By the end of its planned five-year mission, the European Space Agency's Gaia satellite is expected to discover astrometrically and characterize 21,000 ± 6000 giant planets and brown dwarfs with
should be found around solar-type dwarf stars that span the metallicity range of the Milky Way's thin disk. This prediction will soon be tested at an unprecedented scale. By the end of its planned five-year mission, the European Space Agency's Gaia satellite is expected to discover astrometrically and characterize 21,000 ± 6000 giant planets and brown dwarfs with  and
and  (Perryman et al. 2014). This sample of giant planet and brown dwarf mass measurements will be nearly 100 times larger than the sample currently available and extend to the more common intermediate-period objects lacking in my sample. For these reasons, Gaia will provide the definitive test of this prediction that planets with
(Perryman et al. 2014). This sample of giant planet and brown dwarf mass measurements will be nearly 100 times larger than the sample currently available and extend to the more common intermediate-period objects lacking in my sample. For these reasons, Gaia will provide the definitive test of this prediction that planets with 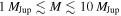 should preferentially be found around metal-rich solar-type dwarf stars, while brown dwarfs with
should preferentially be found around metal-rich solar-type dwarf stars, while brown dwarfs with 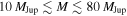 should be found around solar-type dwarf stars that span the metallicity range of the Milky Way's thin disk.
should be found around solar-type dwarf stars that span the metallicity range of the Milky Way's thin disk.
5. Conclusion
Celestial bodies with  preferentially orbit metal-rich solar-type dwarf stars, while celestial bodies with
preferentially orbit metal-rich solar-type dwarf stars, while celestial bodies with 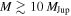 do not preferentially orbit metal-rich solar-type dwarf stars. A preference for metal-rich host stars is thought to be a property of objects formed like giant planets through core accretion, while objects formed like stars through gravitational instability should not prefer metal-rich primaries. As a result, these data suggest that core accretion rarely forms giant planets with
do not preferentially orbit metal-rich solar-type dwarf stars. A preference for metal-rich host stars is thought to be a property of objects formed like giant planets through core accretion, while objects formed like stars through gravitational instability should not prefer metal-rich primaries. As a result, these data suggest that core accretion rarely forms giant planets with 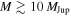 and objects more massive than
and objects more massive than 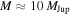 should not be thought of as planets. Instead, objects with
should not be thought of as planets. Instead, objects with 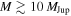 formed like stars through gravitational instability. An upper limit of
formed like stars through gravitational instability. An upper limit of 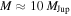 to the mass of planets can only be accommodated in either low-viscosity or low-mass protoplanetary disks. In either case, both Type I and Type II migration are an order of magnitude slower than traditionally assumed. For that reason, these results may point toward the solution of both the Type I and Type II migration problems. Finally, these observations put the definition of a planet as a secondary with
to the mass of planets can only be accommodated in either low-viscosity or low-mass protoplanetary disks. In either case, both Type I and Type II migration are an order of magnitude slower than traditionally assumed. For that reason, these results may point toward the solution of both the Type I and Type II migration problems. Finally, these observations put the definition of a planet as a secondary with 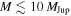 formed via core accretion on a solid observational basis for the first time.
formed via core accretion on a solid observational basis for the first time.
I thank Andy Casey, Greg Laughlin, Margaret Moerchen, Josh Simon, and Josh Winn for insightful comments. This research has made use of NASA's Astrophysics Data System Bibliographic Services, the SIMBAD database, operated at CDS, Strasbourg, France (Wenger et al. 2000), and the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
Software: mclust (Fraley et al. 2012), R (R Core Team 2017), TOPCAT (Taylor 2005).
Appendix A: API Call for Sample Selection
The following URL can be used to reproduce my initial selection with the API available from the NASA Exoplanet Archive: http://exoplanetarchive.ipac.caltech.edu/cgi-bin/nstedAPI/nph-nstedAPI?&table=exoplanets&select&=pl_hostname,ra,dec,st_mass,st_masserr1,st_masserr2,st_metfe,st_metfeerr1,st_metfeerr2,pl_name,pl_letter,pl_bmassj,pl_bmassjerr1,pl_bmassjerr2,pl_massj,pl_massjerr1,pl_massjerr2,pl_disc_refname,pl_disc_reflink,pl_def_refname,pl_def_reflink&where=pl_tranflag=1 and pl_rvflag=1 and pl_massj>=0.1&order=pl_bmassj.
Appendix B: Details of Clustering Algorithms
B.1. Hierarchical Clustering
I use the hclust function in R for hierarchical clustering (R Core Team 2017). That implementation follows the algorithm of Murtagh (1985).
- 1.Calculate the set of
 dissimilarities between n objects.
dissimilarities between n objects. - 2.Identify the smallest dissimilarity dik.
- 3.Combine objects i and k. That is, replace the two objects with a new object,
 , and update all other dissimilarities such that for all objects
, and update all other dissimilarities such that for all objects  the dissimilarity
the dissimilarity  . Delete the dissimilarities
. Delete the dissimilarities  and
and  .
. - 4.Return to Step 2 while the number of objects remaining is greater than two.
This algorithm requires the specification of a dissimilarity metric, and I use the Euclidean distance between each object.
B.2. k-means Clustering
I use the kmeans function in R for k-means clustering (R Core Team 2017). That implementation follows the algorithm of Hartigan & Wong (1979).
- 1.Pick k objects from the n objects to be clustered.
- 2.Assign each object to a cluster by placing each it in the cluster, ki, that has the centroid with the smallest dissimilarity.
- 3.Recalculate the centroid of each cluster.
- 4.Return to Step 2, unless changes in the cluster centroids are small.
This algorithm requires the specification of a dissimilarity metric, and I use the Euclidean distance between each object.
B.3. Gaussian-model Clustering
Footnotes
- 1
The p-values produced by the Kolmogorov–Smirnov test are not generated by comparison with a Gaussian distribution, so I only give a numerical value of σ to aid in the comparison of this result to those of previous studies.
- 2
See Baruteau et al. (2016) for a comprehensive review.
- 3
The frequent occurrence of low-mass stars in Doppler-selected samples of high-mass brown dwarfs has also been seen by Wilson et al. (2016).